恒常法のS字カーブフィッティングについて．

2003/06/20　梶本裕之

心理物理実験の代表的な手法である恒常法．実験手法自体の説明は本に譲るとして，そこで使われるカーブフィッティングを式で説明しているものが少ないようなので補足．

なおここではEXCELとMatlabを使っているが，よりフィッティングに適したソフト(カレイダグラフ等)を使ったほうが楽．

前置き：課題例

まず課題例から．人が指先で凸エッジラインをなぞったとき，エッジ幅をどの程度識別できるかどうかを調べた．標準(Standard)刺激として4mm幅のエッジ，比較(Comparison)刺激として2〜6mm幅のエッジを並べ，二つのエッジを続けてなぞったときにどちらをより『太い』と感じるかを2件法で回答させた．一種類の比較刺激に対して20回の実験を行った．

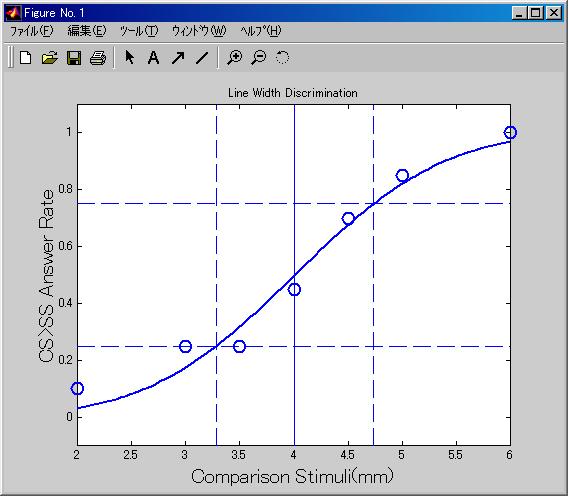
すると次のような結果を得た(データは適当なにせもの)．

このデータから引き出したい情報は次の2点である．

１．回答率が50%となる比較刺激の量．主観的等価点(point of subjective equality，PSE)．この実験の場合は当然4.0mm付近であり，それほど大きな意味を持たない．他の実験では標準刺激と比較刺激で物理的に異なる刺激であったり，何らかの偏りの生じる条件があったりすることが多く，そうした影響を調べる場合に主観的等価点を求めることが重要となる．

２．明瞭に幅の違いを認識できるための幅の差．弁別閾(difference threshold)．例えば75%の確率で正答できる線幅の違いを「弁別確率75％の元での弁別閾」等と呼ぶ．グラフから3mm以下，あるいは5mm以上であれば明瞭に区別できているようである．

これらの情報を引き出すためには何らかのカーブフィッティングを行う必要がある．多くの実験で，比較刺激の値をx，そのときの回答確率をyとした場合に次に定義される正規累積分布関数がよく当てはまることが知られている．

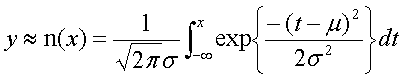
カーブフィッティングの目的は未知パラメータμとσを求めることである．計算すると分かるとおり，μは主観的等価点に等しく（g(x=μ)=0.5），σは弁別閾の大きさに比例する．

良く用いられる最小二乗フィッティング方法

μ=0，σ=1の場合を標準正規累積分布関数と呼ぶ．

これは単調増加関数であり，逆関数が存在する．逆関数は陽の式には表せないが，正規累積分布関数の数表を使って求めることが出来る．これをと表す．例えばEXCELではNORMSINV，Matlabではerfで定義される（erfの定義は若干異なるので後で述べるような変形が必要．もしStatistics Toolboxが入っているならnorminv）．

n(x)とn_std(x)の関係は以下のとおり．

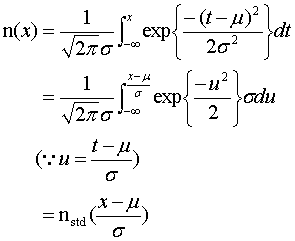
今，比較刺激の値が，そのときの回答確率がだったとする．するとx, yの関係が正規累積分布関数でフィッティング出来るという事は

(1)

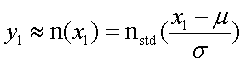
ということであるから，

(2)

となる．先ほど述べたとおりは数表により求められる値である（これをz値と呼ぶ．例えばEXCELではNORMSINV(p)とすればよい）．全てのデータに関して同じことをすれば

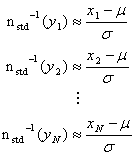
を新たな測定値y，，−を新たな未知数a，bと見なせば，これは単なる線形の最小二乗問題(y=ax+b)であり，直線フィッティングによってパラメータを決定することが出来る(EXCELではグラフデータの右クリックで数式フィッティングを選択できる)．

この方法の大きな欠点は，回答確率が０または１に極めて近いときz値が極めて大きな値をとり，フィッティングに馬鹿らしく大きな影響を与えてしまうことである．Muller-Urban法と呼ばれる手法ではこれを改善するために回答確率0または1付近での最小二乗フィッティングの重み付けを変える．しかしそもそもこういう問題が生じた原因は標準正規累積分布関数の逆関数を使った強引な変換(上式の(1)に含まれる誤差が式(2)で拡大される)にあり，門外漢にはなんとも座りの悪い感じを抱かせる．

回答確率が０または１に極めて近い部分をフィッティングに使わないようにすれば，この方法はそれなりに上手くいくようである(実験としても主観的等価値点付近の刻みを小さくしてデータを多く取るべきである)．以下にそのようにした場合のEXCELによる直線フィッティング結果を載せる．比較刺激が6mmの場合に回答率が1，すなわちz値が発散してしまうため，6mmでの値を除外してフィッティングを行う．

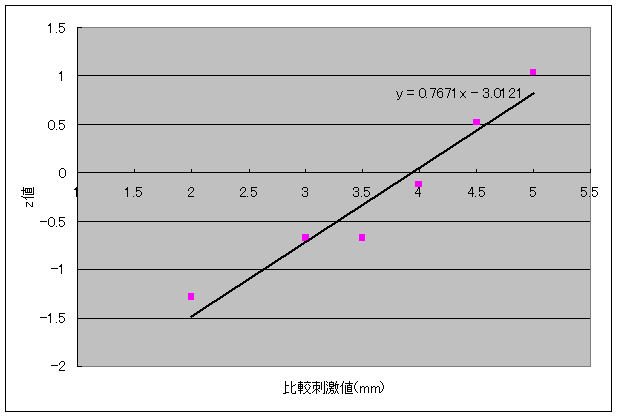
直線フィッティングの結果がa=0.7671, b=-3.0121であるから，前の式からσ= 1.3036，μ= 3.9266と求まる．これによって得られる正規累積分布関数と元データを以下に載せる．それなりに合っている様子が見て取れる．

そもそも正規累積分布を用いること自体に根拠があるわけではないのでこれ以上フィッティングの精度を上げる意味は薄い．そのため手作業でσ，μをいじってフィッティングしたとしてもひどい間違いというわけではない．

個人的に用いている最小二乗フィッティング方法

上に上げた方法が個人的に気持ち悪いため，次のような方法でフィッティングしている(積極的に薦めるものではない)．

未知パラメータμ，σがある値μ₀，σ₀である場合の二乗誤差を数値的に計算する関数を定義する．

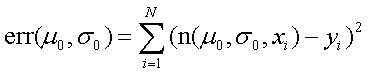
ただしx_i,g_iは比較刺激の値および回答確率である．

二乗誤差err(μ,σ)が最小になるようにμ₀，σ₀を変動させる．これは関数の大域的最小点を求める問題であり，多くの数値解法が存在する．Matlabを使う場合はfminsearch関数等を使うことで極小点を求めることが出来る．極小点が大域的最小点であるかどうかという不安は多少あるが，グラフを見れば大体のμ，σの値を推定でき，初期値をその推定値にすれば良い初期値から出発することになり，まず問題なく収束する．こうして数値的にμ，σを求めることが出来る．少なくとも最小二乗の定義に忠実な方法ではある．

はEXCELではNORMDIST，Matlabではerf関数の変形(Statistics Toolboxがインストールされているならnormcdf)で求めることが出来る．ここではMatlabを使うので，erf関数による表現を求めておく．

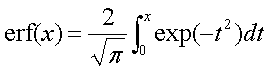
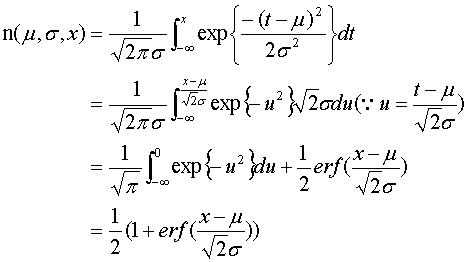
実際のMatlabソースは以下のようになる．まずerr関数はerr.mというファイルに次のように定義する．

===========ここから============

function ret = err(x,cs,p)

sigma = x(1);

mu = x(2);

a = p - 0.5 - 0.5*erf((cs - mu)/(sqrt(2)*sigma));

ret = sum(a.*a);

===========ここまで============

次に極小解を求めるプログラムは次のようになる．

===========ここから============

%恒常法によりデータをフィッティングし、閾値等を求める。

%標準刺激は4mm,比較刺激は2mm〜6mm

%比較刺激Comparison Stimuli

cs = [2.0,3.0,3.5,4.0,4.5,5.0,6.0];

%比較刺激のほうを高いと答えた割合

ans = [0.10, 0.25, 0.25, 0.45, 0.70, 0.85, 1.00];

%データのプロット

p = ans;

hold off;

figure(1);plot(cs,p,'o','LineWidth',2,'MarkerSize',10);

%fminsearch関数により最小二乗法フィッティング

%σ，μとして，適当と思われる初期値1,mean(cs)

%を与える．

OPTION = [];

X = fminsearch('err',[1,mean(cs)],OPTION,cs,p);

sigma = X(1)

mu = X(2)

%75%弁別閾値を求める．

bound025 = erfinv(0.25*2-1)*sqrt(2)*sigma + mu

bound075 = erfinv(0.75*2-1)*sqrt(2)*sigma + mu

hold on;

%フィッティングデータをプロット

cs2 = [min(cs):(max(cs)-min(cs))/100:max(cs)];

p2 = 0.5 + 0.5 .* erf((cs2 - mu)./(sqrt(2)*sigma));

plot(cs2,p2,'LineWidth',2);

%75パーセント弁別閾を描画

plot([min(cs),max(cs)],[0.25,0.25],'--');

plot([min(cs),max(cs)],[0.75,0.75],'--');

plot([bound025,bound025],[-0.1,1.1],'--');

plot([mu,mu],[-0.1,1.1]);

plot([bound075,bound075],[-0.1,1.1],'--');

axis([min(cs),max(cs),-0.1,1.1]);

xlabel ('Comparison Stimuli(mm)','FontSize',15);

ylabel ('CS>SS Answer Rate','FontSize',15);

title('Line Width Discrimination');

===========ここまで============

ついでに75%閾値を求めるためにerfの逆関数であるerfinvを用いていることに注意．これは次のように計算されている．

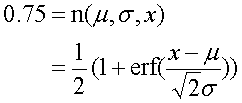
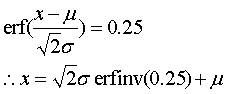
下側閾値は0.75の代わりに0.25とすればよく

で求まる．

Matlabコマンドラインの出力は次のようになり，

フィッティング結果は次のようになる．前のものと比べて劇的に良くなったようには見えず，要は気分の問題である．